(This article is written for study purposes. Please be aware that there may be incorrect information.)
Conference on Computer Vision and Pattern Recognition (CVPR) 2017
https://arxiv.org/abs/1612.00593
1. Introduction
Typical convolutional architectures require highly regular input data formats (e.g. Image Grids, 3D voxels)
However, Point Clouds or Meshes are not in regular format. Therefore, most researchers transform such data into regular 3D Voxel grids or collections of images.
-> This renders the data unnecessarily big

PointNets represent a different input representation for 3D geometry using simply Point Clouds.
PointNets take the Point Clouds directly as the input and outputs the labels for the entire input or part labels/per point segment for each point of the input.
2. Problem Statement
Point Cloud is represented as a set of 3D points {Pi | i = 1,...,n} that only use the (x, y, z) coordinates.
For the object classification task, the input point cloud is either 1. directly sampled from a shape or 2. pre-segmented from a scene point cloud.
PointNet outputs n x m scores for each of the n points and each of the m semantic sub-categories.
3. Deep Learning on Point Sets
3.1 Properties of Point Sets
Our input has 3 main properties.
1. Unordered
-> Point Cloud is a set of points without a specific order.
2. Interaction among points.
-> Points are not isolated, and neighboring points form a meaningful subset. Therefore, the model needs to capture local structures from nearby points, and the combinatorial interactions among local structures.
3. Invariance under transformations
-> The learned representation of the point set should be invariant to certain transformations.
3.2 PointNet Architecture
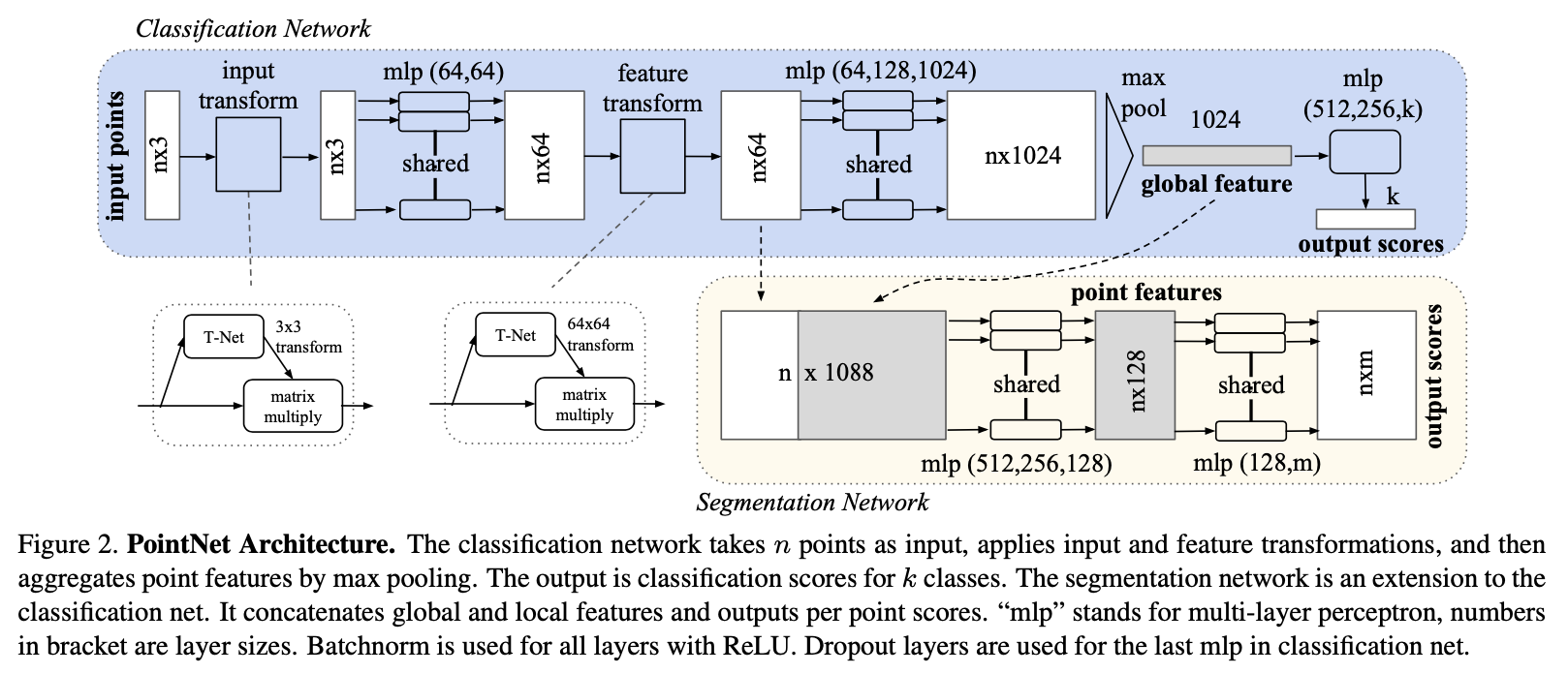
PointNet has 3 key modules:
1. The max-pooling layer as a symmetric function to aggregate information from all the points.
2. A local and global information combination structure
3. Two joint alignment networks that align both input points and point features.
Symmetry Function for Unordered input
The idea is to approximate a general function defined on a point set by applying a symmetric function on transformed elements in a set.

We approximate h by a multi-layer perceptron network and g by a composition of a single variable function and a max pooling function.
Through a collection of h, we can learn a number of f's to capture the different properties of the set.
Local and Global Information Aggregation
Point segmentation requires a combination of local and global knowledge. The solution for this can be seen in Figure 2 (Segmentation Network)
After the computation of the global point cloud vector, we feed it back to per point figures by concatenating the global feature with each of the point features. As a result, the point feature is aware of both the local and global information.
With this modification, PointNet is able to predict per point quantities that rely on both the local geometry and global semantics.
Joint Alignment Network
Since the semantic labeling of a point cloud has to be invariant, we expect that the learnt representation by our point set is invariant to geometric transformations.
This paper does not invent any new layers and no alias is introduced as in the image case.
PointNet predicts a affine transformation matrix by a mini-network (T-net) and apply this transformation to the coordinates of input points. The mini-network resembles the big network, composed by basic modules of point independent feature extraction, max pooling and fully connected layers.
(Affine Transformation -> A linear mapping method that preserves points, straight lines, planes. Typically used for the correction of geometric distortions or deformations)
This idea can be extended in the alignment of feature space. However, the transformation matrix in the feature space (64 x 64) has a higher dimension than the spatial transform matrix (3 x 3), making it more difficult to optimize. Therfore, we need to add a regularization term to the softmax training loss. By adding the regularization term, the optimization becomes more stable, and the model achieves a better performance.
(Feature Space -> An abstract space where each pattern example is represented as point in the n-dimensional space.)

A -> Feature Alignment Matrix predicted by T-net.


