Graph of Thoughts: Solving Elaborate Problems with Large Language Models

GDSC ML 파트 멤버로 처음 쓰는 블로그입니다. 영어로 블로그 작성한 점 양해 부탁드립니다..

리뷰하고자 하는 논문은 Graph of Thoughts 논문으로, Chain-of-Thought의 후속 논문이며, Graph를 사용해서 Latency, Performance를 개선한 것이 유의미한 결과입니다. 

https://arxiv.org/pdf/2308.09687.pdf 

Introduction

Chain-Of-Thought → Includes the intermediate steps of reasoning within the prompt

Fundamentally more powerful prompting can be achieved by enabling LLM thoughts to form an arbitrary graph structure

 

Brains form complex networks, with graph-like patterns such as recurrence.

⇒ Graph-enabled transformations bring a more powerful prompting when applied to LLM thoughts, but it is not expressible with CoT

⇒ Therefore, the authors propose Graph of Thoughts (GoT)

 

Graph of Thoughts’ Main Contributions

1. Enhances LLM’s capabilities through networked reasoning.
   • Graph abstraction by GoT can generalize to more complex thought patterns, without any model updates
2. Designed a modular architecture for implementing GoT
   • Fine-grained control over individual thoughts
   • Architecture can be seamlessly extended with novel thought transformations, patterns of reasoning, and LLM models
3. Implemented use cases using graph-based paradigm
4. Better than the SOTA models
5. ⇒ GoT is great for tasks that can be decomposed into smaller subtasks
6. New metric for evaluating prompting → Volume of a thought

Background

Pretrained language model (LM) with parameters ⇒ $p_\theta$

LLM thoughts ⇒ Lowercase letters ($x, y, z$)

→ thoughts examples) A paragraph, a document, a block of code

 

Input-Output (IO)

Using an LLM to turn an input sequence $x$ into the output $y$ directly (without intermediate thoughts)

 

Chain-of-Thought (CoT)

Introduces intermediate thoughts ($a_1, a_2, ...$) between $x$ and $y$. This enhances various LM tasks over the IO baseline

 

Multiple CoTs

Generating $k$ CoTs, and return the one with the best output

⇒ Enhances CoT because it explores different reasoning paths. However, does not offer local exploration with a path (backtracking)

 

Tree of Thoughts (ToT)

Modeling the process or reasoning as a tree of thoughts

Single tree node → Partial solution

Thought generator constructs a given number $k$ of new nodes

State evaluator generates scores for each new node.

Extending the tree is done by a search algorithm (BFS, DFS)

GoT Framework

GoT is modeled as ($\mathcal{G}, \mathcal{T}, \mathcal{E}, \mathcal{R}$)

⇒ $\mathcal{G}$ : LLM reasoning process, $\mathcal{}$$\mathcal{T}$ : Potential thought transformations, $\mathcal{E}$ : Evaluator function to obtain scores of thoughts, $\mathcal{R}$ : Ranking function to select most relevant thoughts

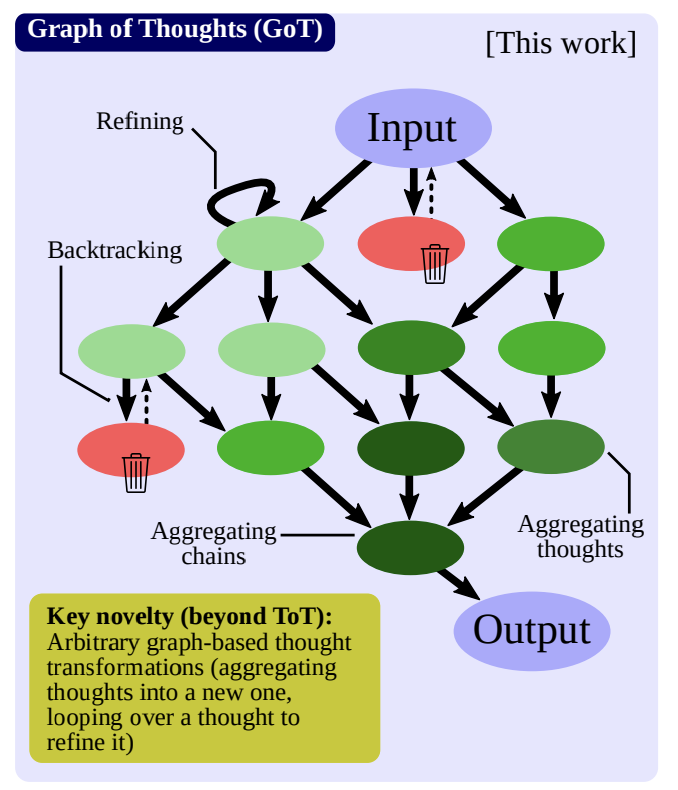
1. Reasoning Process

Model as a directed graph $G = (V, E)$

($V$ : a set of vertices, $E \subseteq V \times V$ : a set of edges)

The vertex contains a solution to a problem at-hand

 

Graph nodes belong to different classes in certain use cases

⇒ GoT uses a heterogeneous graph $G= (V, E, c)$ to model the LLM reasoning. $c$ maps vertices $V$ into their respective classes $C$.

2. Transformations of Thoughts

The transformation can be modeled as $\mathcal{T}(G, p_\theta)$ where $G = (V,E)$ is the graph reflecting the current state, and $p_\theta$ is the used LLM.

 

$\mathcal{T}$ modifies $G$ by adding new vertices and their edges

 

For the expressiveness of GoT, we enable the user to explicitly remove thoughts, by specifying the corresponding vertices and edges to be removed. The specific form of $\mathcal{T}$ and how it impacts $G$ depends on a specific transformation.

 

There are three primary graph-enabled thought transformations

 

Aggregation Transformations

Aggregate arbitrary thoughts into new ones to reinforce the advantages while eliminating the disadvantages ⇒ Only one new vertex is created

⇒ aggregating reasoning paths is enabled

 

Refining Transformations

Refining of a current thought $v$ by modifying its content : $V^{+} = \{\}$ and $E^{+} = \{(v, v)\}$

 

Generation Transformations

Generate one or more new thoughts based on an existing single thought $v$

3. Scoring & Ranking Thoughts

Thoughts are scored to check whether the current solution is good enough. Score is modeled as a general function $\mathcal{E}(v, G, p_\theta)$, where $v$ is a thought to be evaluated

⇒ The whole reasoning process ($G)$ is used for maximum generality

GoT can also rank thoughts, which is modeled with function $\mathcal{R}(G, p_\theta, h)$ where $h$ is the number of the highest ranking thought.

System Architecture

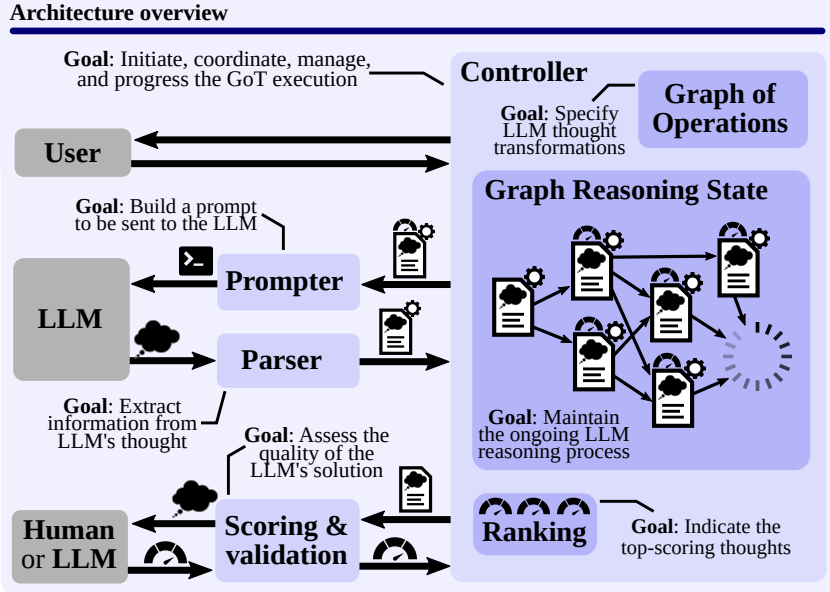
Prompter

Prepares the prompt to be sent to the LLM, and is responsible for specifying the encoding of the graph structure of the prompt

⇒ GoT enables the user to implement case-specific graph encodings by providing full access to the graph structure

Parser

Extracts information from LLM’s thoughts

⇒ Parser constructs the thought state

Scoring & Validation

Verifies whether the LLM’s thought satisfies the potential correctness conditions. Depending on the score, the module may consult the LLM

Controller

1. Implements strategy to select thoughts from the GRS structure
2. Selects what transformations should be applied to which thoughts
3. Passes information to the prompter
4. Decides whether the whole process should be finalized

GoO & GRS

The user constructs a GoO instance (Graph of Operations), prescribing the execution plan of thought operations

⇒ GoO is a static structure that is constructed once (before execution)

Each operation object knows the predecessor and successor, and a instance of GoO maintains the continually updated information about the LLM reasoning process.

Example Use Cases

1. Sorting
2. Set Operations
3. Keyword Counting
4. Document Merging

The Latency-Volume Tradeoff

Volume : The number of preceding LLM thoughts that could have impacted t

(volume of t - number of thoughts from which there exists a path to t)

총평

사람의 thought을 graph로 생각해서 적용한 논문으로 기존의 CoT보다 latency와 volume면에서 향상된 성능을 보임

궁극적으로 어떻게하면 더 최적화를 할 수 있을지가 최종목표가 될 거 같음